複屈折とは?複屈折測定の基本(1/4)
複屈折の理解から当社装置の計測原理や特徴を4つの記事でまとめています
1.複屈折とは?複屈折測定の基本
光の三要素
①振幅:明るさ
![]()
②波長:色
![]()
③振動方向:偏光
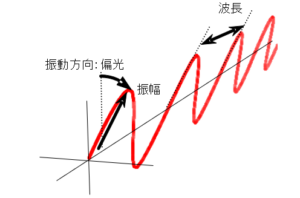
他の2要素と異なり、偏光は肉眼で識別できないので直感的な把握が比較的難しい。
しかしながら、液晶パネルなどに広く利用されている。
偏光と偏光子を使った偏光計測の基本原理
偏光子を回して透過光量の変化を観察
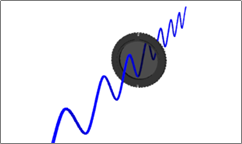
入射光の偏光 ∥ 偏光子の透過軸 → 100%透過
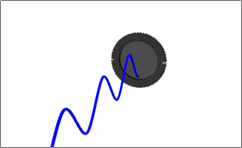
入射光の偏光 ⊥ 偏光子の透過軸 → 0%透過
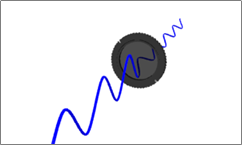
45度の場合… → 50%透過
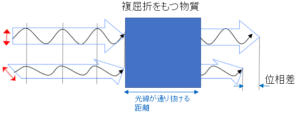
複屈折とは:偏光と位相差について
屈折率とは:光の通り易さ
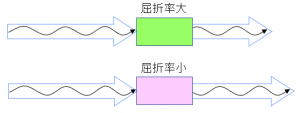
屈折率の大きい物質ほど通り抜けるのに時間がかかる。
※光学距離=屈折率×長さ
屈折率1.5のガラス中では、光の伝播速度は1.5分の1。
複屈折とは:偏光により屈折率が違う状態
| 材料 | 常光 | 異常光 | 複屈折値(⊿n) |
|---|---|---|---|
| 方解石 | 1.6584 | 1.4864 | 0.172 |
| 水晶 | 1.5443 | 1.5534 | 0.0091 |
| サファイア | 1.768 | 1.76 | 0.008 |
| 水 | 1.309 | 1.313 | 0.004 |
位相差=複屈折×距離
ここでは同一物質の同一箇所を、異なる偏光が通過することを想定。
従って距離は一定 → 位相差∝複屈折
複屈折が偏光状態に及ぼす影響
偏光成分の位相差とトータルの偏光状態
直交する2偏光成分の足し合わせで、あらゆる偏光状態は記述できる。
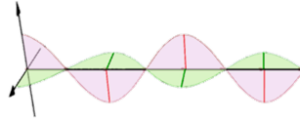
①同位相
※赤の波が最大値のとき、緑の波も最大値(色は波長とは無関係)
直線偏光

②位相差90度
※赤の波が最大値のとき、緑の波が0
円偏光
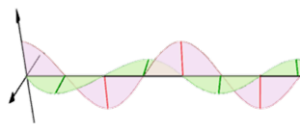
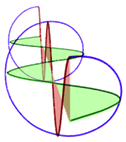
※直交する2偏光の位相差が、偏光状態を様々に変化させる。
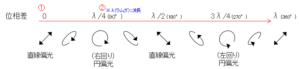
複屈折を有する物質は、透過光の偏光状態を変化させる
【複屈折のない透明体】

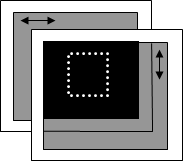
通り抜ける前後で偏光状態は変わらない クロスニコル配置の偏光に挟んでも見えない。
【複屈折のある透明体】

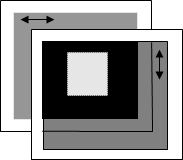
通り抜けた光線の偏光状態が変化する クロスニコル配置の偏光子に挟むと、複屈折に応じて明るく見える。
透過軸方位が直交する2枚の偏光子は光を全遮断する。
↓
この間に複屈折の無い物質を入れても真っ暗なまま。
↓
複屈折のある物質を入れると、その物質で変化された偏光は、
2枚目の偏光子を透過するため明るく見える。
応力による複屈折の発生
複屈折性のない透明材料でも、応力により複屈折が発生する。
これを光弾性効果と呼び、発生する複屈折や位相差の量は応力に比例し、
その比例係数(光弾性係数)は材料ごとに一定。

複屈折= β×応力F (1012Pa)
※つまりT(テラ)Pa単位の応力に光弾性係数を掛けると複屈折量になる。
位相差δ(nm) = β×厚さd (cm)×応力F (105 Pa)
~βは光弾性係数 [ 1012/Pa ]
例えば、厚さ1mmの石英に1MPa(106Pa)の応力で発生する位相差は
3.5×0.1×10=3.5nm
と計算できる。
| 材料 | 光弾性係数(10-12/Pa) |
|---|---|
| 石英 | 3.5 |
| ポリカーボネート | 75 |
| アクリル樹脂 | 6 |
| 一般的な光学ガラス | 0.5 |
| 鉛ガラス | 0.005 |
※水晶の複屈折は約0.01(1.55-1.54)、石英で同等の複屈折が得らる応力は0.003TPa=3GPa。
これ程大きな応力は発生しにくい。一般には光弾性による複屈折は水晶より数桁小さい。
※樹脂成型品の複屈折の大半が、光弾性効果ではなく、分子配向によるとの見解もある。
従って、複屈折や位相差から、単純に内部応力に換算することは殆どの場合適切とはいえない。
しかしながら、成型条件に依存する光学特性の変化であることには変わりが無く、有効かつ重要な評価指標として活用されている。
偏光、複屈折、位相差、光弾性のまとめ
複屈折の分布を評価すると、サンプルの内部歪み分布や分子配向分布などが把握できる。
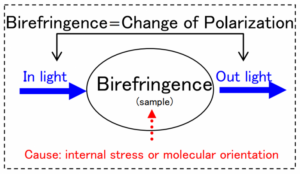
複屈折を持つ物質は、透過した光線の偏光状態を変化させる
↓
従って、透過前後の偏光状態を比較すると、複屈折を評価できる
↓
複屈折の評価技術=偏光計測技術+比較演算技術
※複屈折測定装置は、ハードウェア要素として、偏光計測装置であることが不可欠です。
可能な計算の流れ
①偏光計測
↓
②位相差の算出 (偏光状態の変化から計算)
↓
③複屈折の算出 (位相差とサンプル厚さから計算)
↓
④応力の算出 (複屈折と光弾性係数から計算)
計算上は複屈折や応力まで算出可能です。
しかしながら、以下の理由で、②の位相差データまでの解析に留めることが一般的です。
a.サンプル厚分布データを用いる煩雑さ
b.実用上重要な数値は、複屈折ではなく位相差であることが多いこと
c.複屈折の原因が応力だけである場合が少ないこと
カテゴリ
- #複屈折・応力ひずみ計測ソリューション
- #2次元複屈折評価システム
- #複屈折計測装置
